Have you ever wondered how much water a tank can hold or how many small cubes fit inside a box? Learning about the volume of prisms helps you tackle real-world problems like these.

In this checkpoint, you’ll develop formulas for rectangular and triangular prisms (and any prism shape!) and use them to solve volume problems.

Prisms and Volume

Let’s look at the three most common prisms and their volume formula.

General Prisms: A prism is a 3D shape with two identical and parallel polygonal faces (called bases), and the other faces are rectangles. The cross-section stays the same throughout the length of the prism.

• Volume formula: Volume of a prism= (Area of cross-section) × (length of prism)

Let’s do a question now to practice:

A hexagonal prism has volume 200 cm³. Its length is 10 cm. Find the area of the hexagonal cross-section.

Solution:

Volume = 200 cm³, length = 10cm. Cross-section area = 200 / 10 = 20cm²

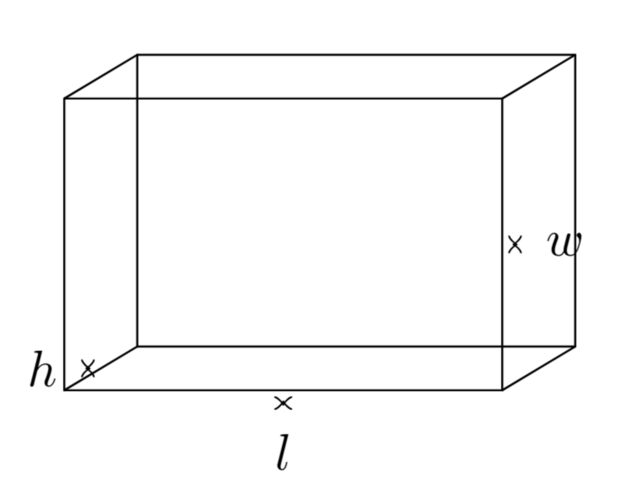
Rectangular Prisms: A rectangular prism is a 3D shape whose faces are rectangles.

• Key dimensions: Length (l), Width (w), and Height (h).
• Volume formula: Volume of a rectangular prism = l × w × h.

Let’s do a question now:

A rectangular prism has a height of 4 cm and a width of 3 cm. If its volume is 144 cm³, find the length. Then, imagine you increase the height to 6 cm but want to keep the same volume and width; what does the length become?

Solution:

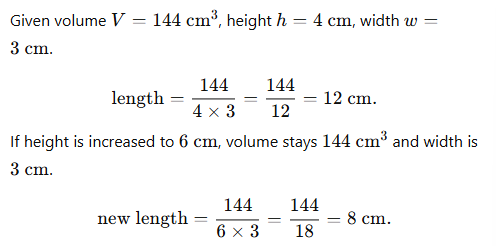
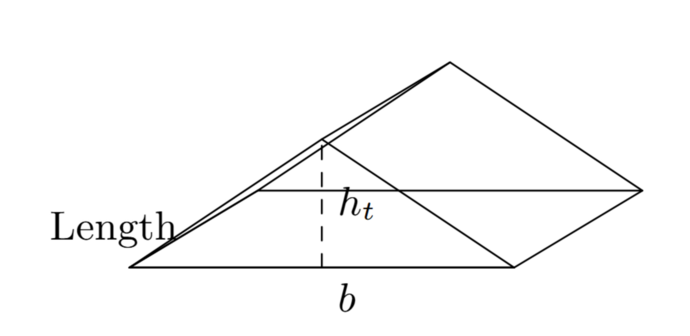
Triangular Prisms: A triangular prism has two identical triangular faces and three rectangular faces.

• Area: If a triangle has base (b) and height (h_t), then its area is ½ × b × h_t The subscript “t” simply denotes that this height is for the triangle in the cross-section (i.e., the height of the triangular face), as opposed to the prism’s overall height or length. It helps distinguish the triangle’s height from other dimensions.
• Length/height of the prism: The distance between the triangular faces (sometimes called the “length” of the prism).
• Volume formula: Volume of a triangular prism = ( ½ × b × h_t) × (length of prism).

Let’s do a question now:

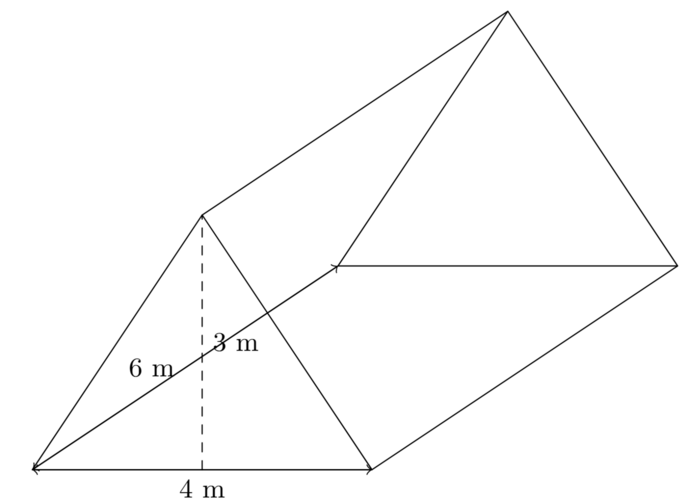
A roof-shaped structure is in the form of a triangular prism (see image below). The cross-section is an isosceles triangle with base 4 m and height 3 m. The “length” of this prism is 6 m.

(a) Find the volume of the structure.
(b) If you only filled half of that space with insulation, how many cubic metres of insulation would you need?

Solution:

(a) Area of cross-section = ½ × 4 × 3 = 6 m². Volume = 6 × 6 = 36 m³.
(b) Half of that space = ½ × 36 = 18 m³.

Approaching Volume of Prism Problems

Here’s how you can approach these problems in your exam:

1. Identify the shape of the cross-section: Determine if it’s a rectangle, triangle, pentagon, or a composite shape.
2. Find or write down the area of that cross-section: For a rectangle: l × w and for a triangle: ½ × b × h. For other polygons (like pentagons, hexagons), the area may be given or can be broken down into simpler shapes (rectangles, triangles).
3. Multiply by the length (or height) of the prism: The volume is the area of the cross-section times the distance between the parallel faces.
4. Rearrange the formula when necessary: If volume is given and you need a missing dimension, solve algebraically for that dimension.

Multi-Part Questions

Remember, in the exam, the questions will be difficult – they may require a combination of concepts. For example, your answer may be required in algebraic form. Let’s do a multi-part question now so that you can look at the approach in action.

Question 1: The Tilted Aquarium

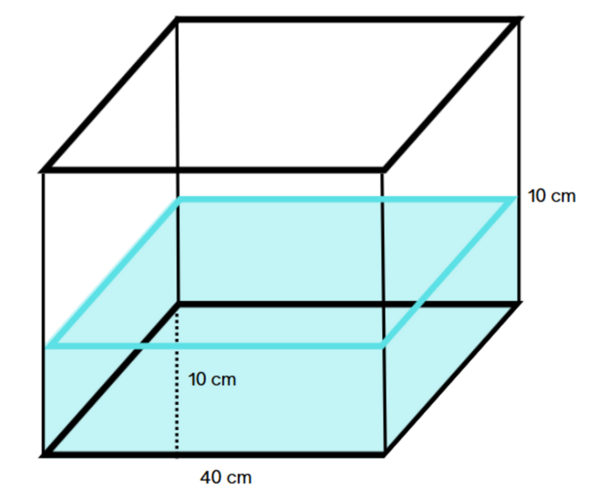
A rectangular aquarium is partially filled with water. The base of the aquarium is a parallelogram. A diagram of the aquarium and its base is shown below:

(Aquarium Diagram - Side View)

(a) The aquarium is filled with water to a height of 10cm, as shown in the side-view diagram. Calculate the volume of water in the aquarium, in litres.

(b) A decorative rock in the shape of a cube is placed in the aquarium and is completely submerged in the water. If 2 extra litres of water is poured once the rock has been placed in the aquarium, and it causes the water level to reach a new height of 17.5cm, what is the length of each side of the rock?

Solution to A

• Base Area: The base is a parallelogram. Base length = 40 cm. Height of parallelogram = 10 cm. Area of base = base * height = 40 cm * 10 cm = 400 cm²
• Volume of Water: Volume = Base Area * Height of water. Volume = 400 cm² * 10 cm = 4000 cm³
• Convert to Liters: 1000 cm³ = 1 L. 4000 cm³ = 4 L

Solution to B

• Volume with Rock: The base area remains constant, with the area of the base being 400 cm². Volume = Base area * Height of water = 400 * 17.5 = 7000 cm³
• Convert to litres = 7000 / 1000 = 7 L.
• Initial volume of just water: 4 L.
• Volume of rock: Total volume - volume of water added after rock - volume of water = 7 - 2 - 4 = 1 L. 1 L = 1000cm³
• Side of rock: Volume of cube = s³. 1000 = s³. s = 10 cm.

Practice time!

Now, it's your turn to practice.

The questions in this checkpoint are provided to give you an introduction to possible questions you may see in your exam. Don't worry too much as you'll continue to build your skills throughout the course.

Click on the button below and start your practice questions. We recommend doing untimed mode first, and then, when you're ready, do timed mode.

Every question has a suggested solutions videos after you complete the question. This video explains to you the steps to take to answer the question and provides tips and tricks.

Once you're done with the practice questions, move on to the next checkpoint.

Now, let’s get started on your practice questions.