Common Units of Measurement & Volume

Measurement is a fundamental part of understanding the world around us, allowing us to quantify physical properties like length, area, and volume. Calculating the perimeter, which is the total distance around a shape, and the area, which is the space enclosed within a shape, are essential skills in geometry. Understanding these concepts will enable you to solve a wide range of practical problems, from designing a garden to working out how much paint is required to redecorate.

At a basic level, you should recall the following:

• For a square/rectangle, the perimeter is the sum of all 4 sides. For area, it is length times width.
• For a triangle, the perimeter is the sum of all 3 sides. For area, it is length times width, divided by 2.

Let’s start with common units:

• Square millimetre (mm²): Very small area (e.g., the area of a small seed).
• Square centimetre (cm²): Small area (e.g., the area of a postage stamp).
• Square metre (m²): Larger area (e.g., the area of a room).
• Square kilometre (km²): Very large area (e.g., the area of a city).
• Hectare (ha): Used for land area (1 ha = 10,000 m²).

Here are common conversions:

• 1 cm² = 100 mm² (because 1 cm = 10 mm, and (10 mm)² = 100 mm²)
• 1 m² = 10,000 cm² (because 1 m = 100 cm, and (100 cm)² = 10,000 cm²)
• 1 km² = 1,000,000 m² (because 1 km = 1000 m, and (1000 m)² = 1,000,000 m²)

Let’s move onto volume. Volume measures the amount of space inside a three-dimensional object.

Here are common units:

• Cubic millimetre (mm³): Very small volume (e.g., the volume of a grain of sand).
• Cubic centimetre (cm³): Small volume (e.g., the volume of a sugar cube). Also known as a millilitre (mL).
• Cubic metre (m³): Larger volume (e.g., the volume of a refrigerator).
• Litre (L): Common for liquid volume (1 L = 1000 cm³).

Here are their conversions:

• 1 cm³ = 1000 mm³ (because 1 cm = 10 mm, and (10 mm)³ = 1000 mm³)
• 1 m³ = 1,000,000 cm³ (because 1 m = 100 cm, and (100 cm)³ = 1,000,000 cm³)
• 1 L = 1000 cm³

Let’s do some simple questions:

• Convert 3 L to cm³.
• Convert 0.5 m³ to cm³.
• A rectangular field has an area of 2 hectares. What is its area in square meters?

Solutions:

• 3000 cm³ (3 L * 1000 cm³/L = 3000 cm³)
• 500,000 cm³ (0.5 m³ * 1,000,000 cm³/m³ = 500,000 cm³)
• 20,000 m² (2 ha * 10,000 m²/ha = 20,000 m²)

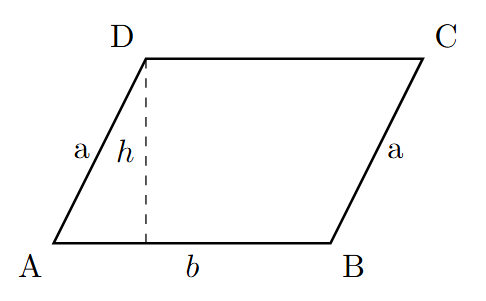
Parallelograms

A parallelogram is a quadrilateral (four-sided shape) with two pairs of parallel sides. The opposite sides are equal in length and the opposite angles are equal.

Here are some formulas when dealing with parallelograms:

• To find perimeter: 2(a + b), where 'a' and 'b' are the lengths of adjacent sides.
• To find area: = base * height (A = b * h)

Note that, the base is any one of the sides. The height is the perpendicular distance from the base to the opposite side.

Let’s do some quick questions:

1. The area of a parallelogram is 48 cm², and its base is 12 cm. What is its height?
2. A parallelogram-shaped field has a perimeter of 100 m. If one side is 30 m long, what is the length of the adjacent side?
3. A parallelogram has an area of 72 cm² and a height of 8cm. Find its base.

Solutions:

1. 4 cm (h = A/b = 48 cm² / 12 cm = 4 cm)
2. 20 m (Let the adjacent side be 'x'. 2(30 m + x) = 100 m; 60 m + 2x = 100 m; 2x = 40 m; x = 20 m)
3. 9 cm (b = A / h = 72 / 8 = 9)

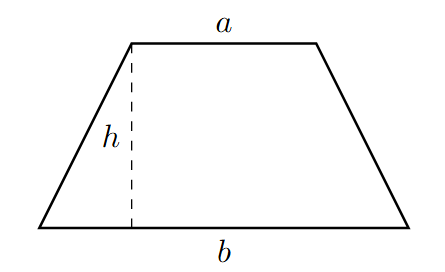
Trapeziums (Trapezoids)

A trapezium (or Trapezoid) is a quadrilateral with at least one pair of parallel sides. Parallel sides are called bases (often labelled 'a' and 'b'). The non-parallel sides are called legs. The height (h) is the perpendicular distance between the bases.

Here are some formulas when dealing with a trapezium:

• Perimeter = sum of all sides.
• Area = (1/2) * (sum of bases) * height or A = (1/2)(a + b)h. Where 'a' and 'b' are the lengths of the parallel sides (bases). 'h' is the perpendicular distance between the bases (height).

Let’s do some quick questions:

1. A trapezium-shaped garden has parallel sides of length 10 m and 15 m, and the perpendicular distance between them is 8 m. Find the area of the garden.
2. A trapezium has an area of 50 cm squared. If the height is 5cm, and one of the parallel sides is 8, work out the length of the other parallel side.
3. Find the area of the trapezium if the lengths of its parallel sides are 12 cm and 18 cm and the perpendicular distance between them is 10 cm.

Solutions:

1. 100 m² (A = (1/2)(10 m + 15 m) * 8 m = (1/2)(25 m)(8 m) = 100 m²)
2. 12 cm (50 = (1/2)(8+b)5 = 1/2 * 5(8+b) = 2.5(8+b); 50/2.5 = 8 + b = 20; 20-8= b = 12)
3. 150 cm². A=(1/2)∗(12+18)∗10 = 0.5 * 30 * 10=150cm².

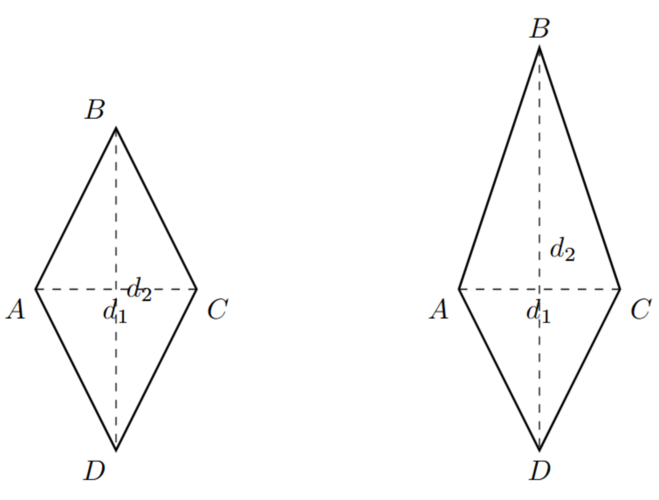
Rhombuses and Kites

A rhombus is a quadrilateral with all four sides equal in length. Opposite sides are parallel, and opposite angles are equal. A rhombus is a special type of parallelogram.

A kite is also a quadrilateral however, it has two pairs of adjacent sides that are equal in length.

Here are some formulas when dealing with these two shapes:

Rhombus

• Perimeter = 4 * side length
• Area = (1/2) * d₁ * d₂, where d₁ and d₂ are the lengths of the diagonals.

Kite

• Perimeter = 2(a + b) , where 'a' and 'b' are the lengths of the non-equal sides adjacent to each other.
• Area = (1/2) * d₁ * d₂, where d₁ and d₂ are the lengths of the diagonals.

Let’s do some simple practice:

1. A rhombus has diagonals of length 10 cm and 12 cm. What is its area?
2. The area of a kite is 36 cm². If one diagonal is 9 cm long, what is the length of the other diagonal?
3. A rhombus shaped tile has an area of 48cm squared, with one diagonal being 8cm long. How long is the other diagonal?

Solutions:

1. 60 cm² (A = (1/2) * 10 cm * 12 cm = 60 cm²)
2. 8 cm (d₂ = (2 * A) / d₁ = (2 * 36 cm²) / 9 cm = 8 cm)
3. 12cm ((1/2) * 8 * d = 48; 4d = 48; d = 48 / 4 = 12 cm)

Questions in the exam aren’t simply going to ask you to calculate the area of a kite and provide you with all you need. Instead, the questions will want you to decide which formula to use, along with figuring out the lengths that you need to calculate it. Remember, it’s likely going to have missing information that you need to piece together, in order to find the answer. Let’s now do some harder questions, the type of questions that require critical thinking:

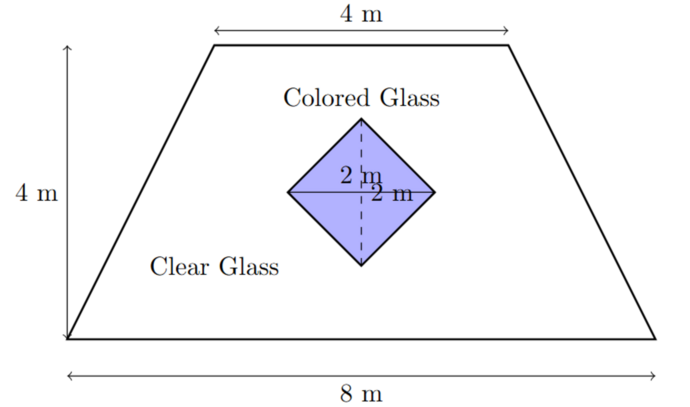
Question 1: The Stained-Glass Window

A craftsperson is making a stained-glass window. The window design consists of a large trapezium-shaped piece of clear glass with a smaller rhombus-shaped piece of coloured glass inlaid in the centre. The dimensions are shown in the diagram below:

The craftsperson wants to cover the clear glass with a special protective film. The film costs $50 per square meter.

What is the total cost of the film required to cover only the clear glass, excluding the coloured glass?

Solution

• Calculate the Area of the Trapezium: The formula for the area of a trapezium is: Area = (1/2) × (Base₁ + Base₂) × Height. Base₁ (Top Side) = 4 m. Base₂ (Bottom Side) = 8 m. Height = 4 m. Area of Trapezium = (1/2) × (4 + 8) × 4 = (1/2) × 12 × 4 = 24 m²
• Calculate the Area of the Coloured Glass (Rhombus). The formula for the area of a rhombus with given diagonals is: Area = (1/2) × d₁ × d₂. Given: Diagonal₁ = 2 m. Diagonal₂ = 2 m. Area of Rhombus = (1/2) × 2 × 2 = 2 m²
• Calculate the Area of the Clear Glass. Clear Glass Area = Area of Trapezium - Area of Rhombus = 24 - 2 = 22 m²
• Calculate the Cost of the Protective Film. The cost of the film is $50 per square meter. Total Cost = 22 × 50 = 1100

Question 2: The Tessellated Tile Pattern

An artist is creating a mosaic for a new community center. The mosaic will be a rectangular section of a wall that is 4 meters long and 2 meters high. The artist plans to use a tessellating pattern composed entirely of identical kite-shaped tiles. Each kite has diagonals of length 20 cm and 10 cm.

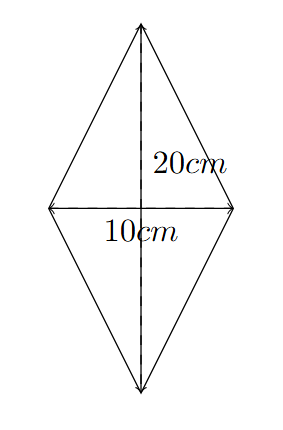
The community centre wants the artist to determine the absolute maximum number of whole tiles, keeping the original shape and dimension.

1. What is the maximum number of whole kite-shaped tiles the artist can use in the mosaic?
2. What is the area of the mosaic wall in square centimetres?

Solution:

• Step 1: Convert Units and Find Kite Area. Convert the wall dimensions to centimetres: 4 meters = 400 cm. 2 meters = 200 cm. Find the area of one kite-shaped tile: Area of a kite = (1/2) * d1 * d2, where d1 and d2 are the lengths of the diagonals. Area of one kite = (1/2) * 20 cm * 10 cm = 100 cm²
• Step 2: Determine the Maximum Number of Whole Kites. Calculate the area of the mosaic wall: Wall area = length * width = 400 cm * 200 cm = 80,000 cm² Divide the Wall area by a single kite: 80,000cm² / 100cm²= 800. Therefore, the maximum number of whole kite tiles is 800.
• Step 3: Calculate Area of Wall in Centimetres. Wall area = length * width = 400 cm * 200 cm = 80,000 cm²

Practice time!

Now, it's your turn to practice.

The questions in this checkpoint are provided to give you an introduction to possible questions you may see in your exam. Don't worry too much as you'll continue to build your skills throughout the course.

Click on the button below and start your practice questions. We recommend doing untimed mode first, and then, when you're ready, do timed mode.

Every question has a suggested solutions videos after you complete the question. This video explains to you the steps to take to answer the question and provides tips and tricks.

Once you're done with the practice questions, move on to the next checkpoint.

Now, let’s get started on your practice questions.

---