Introducing the Circle and its Parts

You've probably seen circles everywhere – from wheels to pizzas! But did you know that circles have some fascinating mathematical secrets? Understanding these secrets is key to solving many exam problems.

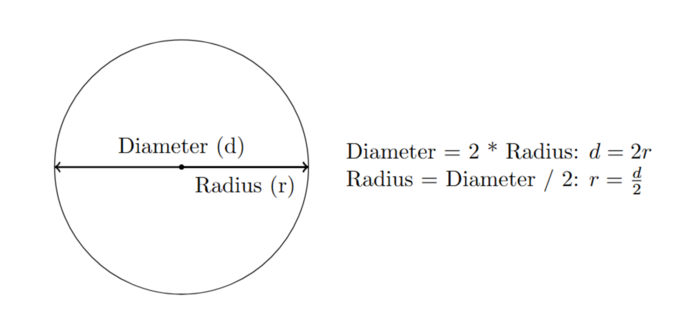
Let's start by exploring the important definitions you'll need (see the diagram below):

• Centre: the middle point of a circle – this is shown by the dot in the diagram. A circle is set of points in a plane that are the same distance from a fixed point
• Radius (r): The distance from the centre of the circle to any point on the circle.
• Diameter (d): The distance across the circle through the centre. It is twice the radius (d = 2r).
• Circumference (C): The distance around the circle (its perimeter).
• Area (A): The amount of space enclosed within the circle.

From the image you’ll see some relationships between the radius and diameter. These are:

• Diameter = 2 * Radius: d = 2r
• Radius = Diameter / 2: r = d/2

Let’s go through some easy questions:

1. A circular pizza has a radius of 10 inches. What is the diameter of the pizza?
2. A bicycle wheel has a diameter of 60 cm. What is the radius of the wheel?
3. The minute hand on a clock is 7 cm long. What is the diameter of the circle traced out by the tip of the minute hand?

Solutions: 20 inches, 30 cm, 14 cm

These relationships between radius, diameter, and centre seem straightforward, but how will they be tested on the exam? Exam questions will likely embed these concepts within more complex, real-world problems. You'll need to recognise when and how to apply these relationships as part of a larger solution, often as a hidden step.

Understanding Circumference

The circumference is the distance around the circle. It's like the perimeter of a polygon, but for a curved shape.

The formula for circumference is:

• C = 2πr (using radius – see how the 2r is actually the formula for diameter!)
• C = πd (using diameter – remember though, if you only have radius, you can still get to diameter!)

Where π (pi): π is a special mathematical constant, approximately equal to 3.14 or 22/7. For most Year 7/8 calculations, using 3.14 or 22/7 is sufficient. For the purposes of the competitive test, we will use the fractional representation of 22/7.

Example: Find the circumference of a circle with a radius of 7 cm. (Use π = 22/7)

C = 2πr = 2 * (22/7) * 7 cm = 44 cm

Let’s do some more simpler practice questions:

1. A circular track has a diameter of 70 meters. What is the distance around the track? (Use π = 22/7)
2. A wheel has a radius of 21 cm. How far does it travel in one complete revolution? (Use π = 22/7)
3. The minute hand of a clock is 3.5 cm long. How far does the tip of the minute hand travel in one hour? (Use π = 22/7)

Solutions: 220 meters (C = (22/7) * 70 = 220); 132 cm (C = 2 * (22/7) * 21 = 132); 22 cm (C = 2 * (22/7) * 3.5 = 22)

Area of a Circle

Area is the amount of space inside a two-dimensional shape. The formula for area of a circle is:

Formula: A = πr²

Where 'A' is the area, 'π' is pi (approximately 3.14 or 22/7), and 'r' is the radius.

Example: Find the area of a circle with a radius of 7 cm. (Use π = 22/7)

A = πr² = (22/7) * (7 cm)² = (22/7) * 49 cm² = 154 cm²

Let’s do some simple practice questions:

1. A circular pizza has a radius of 7 cm. What is its area? (Use π = 22/7)
2. A circular garden has a diameter of 14 m. What is the area of the garden? (Use π = 22/7)
3. A circular table top has a radius of 21 cm. What is its area? (Use π = 22/7)

Solutions:

1. For the circular pizza with a radius of 7 cm, using π = 22/7, the area is calculated as A = (22/7) * 7 * 7; since 7 * 7 = 49, this becomes (22/7) * 49, where the 7s cancel, leaving 22 * 7 = 154, so the area is 154 cm².
2. For the circular garden with a diameter of 14 m, the radius is 14 / 2 = 7 m, and using π = 22/7, the area is A = (22/7) * 7 * 7; since 7 * 7 = 49, this simplifies to (22/7) * 49, where the 7s cancel, giving 22 * 7 = 154, so the area is 154 m².
3. For the circular table top with a radius of 21 cm, using π = 22/7, the area is A = (22/7) * 21 * 21; since 21 * 21 = 441, this becomes (22/7) * 441, and 441 / 7 = 63 (as 21 = 7 * 3, so 441 = 7 * 7 * 9), then 22 * 63 = 22 * (60 + 3) = 1320 + 66 = 1386, so the area is 1386 cm².

Solving Problems with Radius, Diameter, Circumference, and Area

Exam problems may require you to use multiple formulas and relationships to find the answer. Here are some quick tips with how to work backwards.

• From Circumference to Radius/Diameter: If you know C, you can find r: r = C / (2π), If you know C, you can find d: d = C / π
• From Area to Radius: If you know A, you can find r: r = √(A / π) (You may not be expected to do square roots of non-perfect squares at Year 7/8, so questions will be designed accordingly.)

Example: The circumference of a circle is 88 cm. Find its radius. (Use π = 22/7)

R = C / (2π) = 88 cm / (2 * (22/7)) = 88 cm / (44/7) = 88 * (7/44) = 14 cm

Now, let’s do some harder questions, the type of questions that require critical thinking:

Question 1: A Park Fence

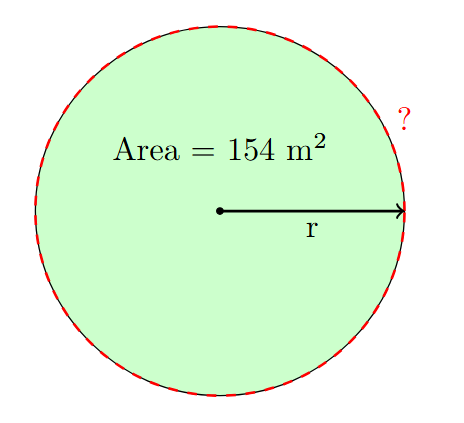
A circular park is to be enclosed by a fence. The area of the park is shown in the diagram below. What is the total length of fence needed, in meters? (Use π = 22/7)

Part A: Find the radius:

• A = πr²
• 154 = (22/7) * r²
• r² = 154 * (7/22) = 49
• r = √49 = 7 m (sometimes the answer will be shown as a square root instead of as a integer)

Part B: Find the circumference:

• C = 2πr = 2 * (22/7) * 7 m = 44 m

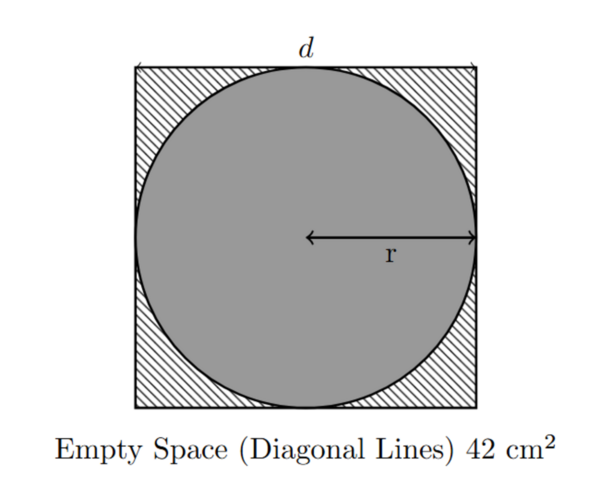
Question 2: The Pizza and the Plate

A circular pizza is perfectly placed inside a square plate, touching all four sides of the plate, as shown in the diagram above. The area of the empty space on the plate (the area not covered by the pizza) is 42 cm².

What is the radius of the pizza, in cm? What is the circumference of the pizza, in cm?

Solution:

1. Let 'r' be the radius of the pizza.
2. Relate radius to the square: The diameter of the pizza (2r) is equal to the side length of the square plate.
3. Area of the square: The side length of the square is 2r, so the area of the square is (2r)² = 4r².
4. Area of the pizza: The area of the pizza is πr² = (22/7)r².
5. Area of empty space: Area of square - Area of pizza = 42 cm²
6. 4r² - (22/7)r² = 42

Simplify the equation:

1. (28/7)r² - (22/7)r² = 42
2. (6/7)r² = 42
3. r² = 42 * (7/6) = 7 * 7 = 49
4. r = √49 = 7

Then, to find circumference - use the formula for circumference: C = 2πr = 2 * (22/7) * 7 = 44 cm

Question 3: The Track Design

An athletics track is designed with two straight sections and two semicircular ends, as shown in the diagram. The total length of one straight section is 90 meters. The total distance around the inside of the track (one lap) is 400 meters. For this problem, use π = 22/7.

(a) What is the diameter, in meters, of each semicircular end of the track? (b) What is the total area enclosed by the inside of the track, in square meters?

Solution for Part A

1. Let 'd' be the diameter of each semicircle.
2. Total length of straight sections: 2 * 90 m = 180 m
3. Length of the circular part: 400 m - 180 m = 220 m
4. Circumference and diameter: The 220 m is the circumference of a full circle with diameter 'd'. C = πd, so 220 = (22/7) * d
5. Solve for d: d ≈ 220 * (7/22) --> d = 10 * 7 --> d = 70 m

Solution for Part B

1. Find the radius: r = d/2 = 70 m / 2 = 35 m
2. Area of the full circle: A = (22/7) * (35 m)² = (22/7) * 1225 m² = 22 * 175 = 3850 m².
3. Area of the rectangle: Length = 90 m, Width = 70 m. Area = 90 m * 70 m = 6300 m².
4. Total area: Total Area = 3850 m² + 6300 m² = 10150 m²

Practice time!

Now, it's your turn to practice.

The questions in this checkpoint are provided to give you an introduction to possible questions you may see in your exam. Don't worry too much as you'll continue to build your skills throughout the course.

Click on the button below and start your practice questions. We recommend doing untimed mode first, and then, when you're ready, do timed mode.

Every question has a suggested solutions videos after you complete the question. This video explains to you the steps to take to answer the question and provides tips and tricks.

Once you're done with the practice questions, move on to the next checkpoint.

Now, let’s get started on your practice questions.

---